Per-Axis Weight Deltas for Efficient Model Serving

As large language models (LLMs) continue to grow in size, serving multiple fine-tuned versions of the same base model becomes increasingly challenging. Each specialized version requires significant storage space and memory, making it expensive to deploy many task-specific models. Recent systems like S-LoRA [1] have shown the importance of efficiently serving thousands of model variants concurrently. While parameter-efficient fine-tuning methods like LoRA [2] store only small adapter modules, full fine-tuning and reinforcement learning post-training often update all model parameters, requiring complete model copies for each variant. When you store these fully fine-tuned models for different tasks (say, one for legal documents, another for medical text, and a third for creative writing), each variant requires its own complete checkpoint. For example, an 8B parameter LLM like Llama-3 requires approximately 15GB per variant in FP16 format. If you're serving dozens of such specialized models, the storage and memory costs quickly become prohibitive. Loading and unloading these checkpoints leads to higher latency and cost when providing inference.

However, fine-tuned models aren't actually that different from their base versions. The weight changes introduced during fine-tuning are typically small and structured. Building on compression-based approaches like BitDelta [3], we developed a method that represents weight differences using only their signs (1 bit per weight) plus lightweight scaling factors. The key innovation is using per-axis scaling (either per-row or per-column) rather than a single global scale for the entire weight matrix.

How It Works

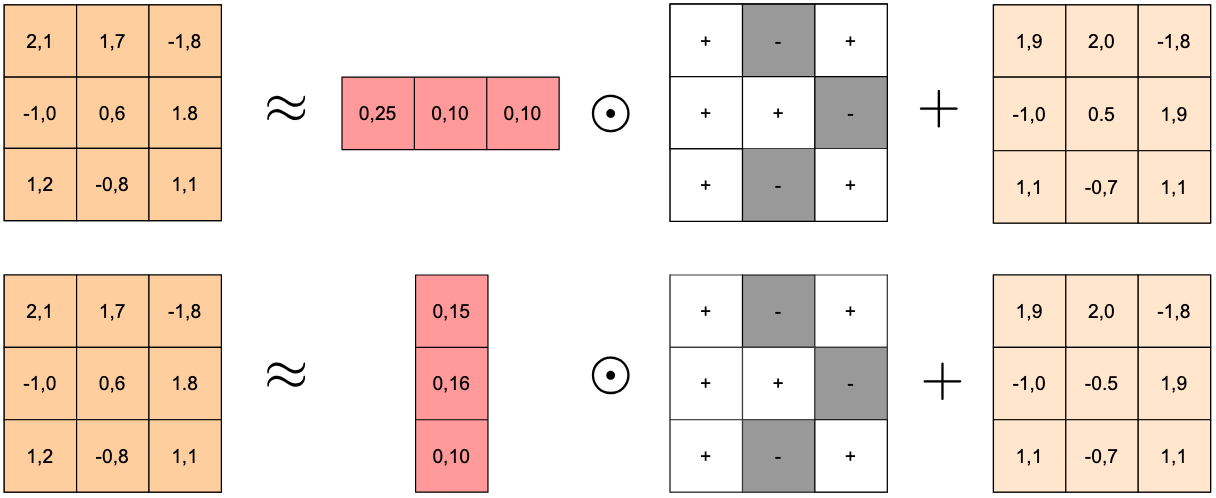
For each layer's weights, we compute the difference between the fine-tuned and base models: $\Delta W = W_{\text{fine-tuned}} - W_{\text{base}}$. We then extract the sign of each weight difference, giving us $B = \text{sign}(\Delta W) \in \{-1, +1\}$. Finally, we learn a vector of scales $\mathbf{v}$ (either one value per row or per column) to reconstruct the fine-tuned weights as $\hat{W} = \mathbf{v} \odot B + W_{\text{base}}$, where $\odot$ represents element-wise multiplication with broadcasting.

The crucial insight is that weight changes during fine-tuning aren't uniform across all dimensions. Some rows or columns of a weight matrix might change significantly, while others barely change at all. A single global scale forces a compromise that either over-scales small changes (adding noise) or under-scales large changes (losing important information). By allowing different scales for different rows or columns, we can better capture these patterns. We automatically select whether to use row or column scaling for each layer based on which reconstructs the model's behavior more accurately.

Rather than trying to match the weights exactly, we focus on preserving what matters: the model's outputs. This follows a similar philosophy to recent quantization methods such as GPTQ [4], which minimize layer-wise output error rather than weight reconstruction error. We use a small calibration dataset (just 50 samples from the C4 dataset [5]) to learn the optimal scales by minimizing the difference between the original fine-tuned model's outputs and our compressed version's outputs: $\mathcal{L} = \frac{1}{n}\|Y - \hat{Y}\|_2^2$. This activation-matching approach ensures that our compressed model behaves similarly to the original, even if the exact weight values differ slightly.

Results and Impact

We evaluated our method by compressing Llama-3.1-8B-Instruct (the fine-tuned version) relative to Llama-3.1-8B (the base model). Here are the zero-shot accuracy results across five standard benchmarks:

Model	ARC-C	ARC-E	HellaSwag	PIQA	Winogrande	Average
Baseline (Full Model)	51.70	81.81	59.06	79.86	73.87	69.26
BitDelta (scalar)	52.55	82.32	59.73	81.22	73.95	69.95
Our Method (per-axis)	53.58	82.99	59.78	80.63	74.19	70.23

Our per-axis approach achieves the highest average accuracy (70.23%), outperforming both the uncompressed baseline and the scalar BitDelta method, while maintaining roughly the same compression ratio. In our experiments with Llama-3.1-8B, the full FP16 model checkpoint is approximately 15 GB, while our compressed delta needs only 3 GB (a 5.4× reduction). While loading a full fine-tuned Llama-3.1-8B model takes about 2.08 seconds on our machine with RTX4090 GPUs, loading and applying our compressed delta on top of an already-loaded base model takes only 0.80 seconds without any specialized kernels. This makes it much faster to switch between different fine-tuned variants on the fly.

Looking Forward

Our method works best when the fine-tuning introduces structured changes that vary across dimensions. For layers where changes are more uniform, a simpler scalar approach might suffice. We're exploring several extensions including blockwise scaling for even finer-grained control, learning the sign patterns rather than just using raw signs, and integration with INT4/FP8 quantization for additional compression.

This research supports the infrastructure behind our AI workflow platform at buildbleu.com. When users create and deploy AI backends using our visual workflow builder, we want them to be able to serve multiple specialized model variants efficiently.

References

[1] Sheng et al., "S-LoRA: Serving Thousands of Concurrent LoRA Adapters", arXiv:2311.03285, 2024

[2] Hu et al., "LoRA: Low-Rank Adaptation of Large Language Models", arXiv:2106.09685, 2021

[3] Liu et al., "BitDelta: Your Fine-Tune May Only Be Worth One Bit", NeurIPS 2024

[4] Frantar et al., "GPTQ: Accurate Post-Training Quantization for Generative Pre-trained Transformers", arXiv:2210.17323, 2023

[5] Raffel et al., "Exploring the Limits of Transfer Learning with a Unified Text-to-Text Transformer", JMLR 2020